İki ispat

Posted on February 15, 2012 by Arkadaş


1 + 3 + 5 + \ldots + (2n-1) = n^2

1 + 2 + 3 + \ldots + (n-1) = {{n}\choose{2}}

(İlki için William Dunham’ın bir kitabını kaynak gösteriyor Wikipedia, o da 2000 yıl önce Eski Yunan’da  biliniyordu bu demiş. İkincisi MathOverflow’dan; Mariano Suárez-Alvarez‘in kendi sorduğu bir soruya verdiği cevaplardan biri. Formülde {n\choose 2} dediği, n‘nin ikili kombinasyonlarının sayısı.)

This entry was posted in Uncategorized. Bookmark the permalink.

4 Responses to İki ispat

  1. Özlem Beyarslan says:
    August 28, 2012 at 8:05 am

    Bu iki sekli bugun verdigim sayma adli lise dersinde tahtaya cizdim. Ikincisini bulan cikmadi henuz.

    Reply
  2. Arkadaş says:
    August 28, 2012 at 8:29 am

    İlkinde sonucun neden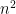 n^2 olduğunu biraz daha açsan ikincisine de faydası olur mu acaba?

    Reply
  3. Yılmaz Aksoy says:
    September 6, 2014 at 4:51 am

    İkinci şekil çok hoşuma gitti ya. Eşleşmelerin birebir (ve örten) olduğunu görünce ne kadar aptalmışım ifadesi belirdi yüzümde bir an.

    Reply
  4. Arkadaş says:
    September 6, 2014 at 4:58 am

    O çok hoş gerçekten, bir an duraksatıyor ama sonra gülümsetiyor, vay be dedirtiyor :)

    Reply

Leave a Reply to Arkadaş Cancel reply